
풀이
LIS문제의 원리를 잘 다룬 문제이다.
기존에 O(N^2) 방식으로 LIS를 구할 때, 비연속 LIS 길이를 찾을 수 있었다.
[백준 11053] 가장 긴 증가하는 부분 수열 [Python]
풀이 LIS (Longest Increasing Subsequence)는 최장 증가 부분 수열로, N개의 원소에 대해 요소를 골라 만든 부분 수열을 만들 때 각 원소가 이전 요소보다 큰 원소로 이루어진 부분 수열을 의미한다. 즉, 가
kyr-db.tistory.com
LDS를 찾을 때도 마찬가지로 같은 방식을 사용했다.
[백준 11722] 가장 긴 감소하는 부분 수열 [Python]
풀이 일전에 풀었던 LIS문제에서 사용한 방법을 응용해 풀이할 수 있다. [백준 11053] 가장 긴 증가하는 부분 수열 [Python] 풀이 LIS (Longest Increasing Subsequence)는 최장 증가 부분 수열로, N개의 원소에
kyr-db.tistory.com
그렇다면 이번 문제에서 주어지는 LBS(Longest Bitonic Subsequence)는 어떻게 구해야 할까?
구간별 LIS, LDS, LBS 길이를 아래 그림을 통해 살펴보자.

결국 구간별로 비연속적 증가 또는 감소하는 길이를 탐색하는 과정이다.
1 ~ N 번 요소에 대한 LIS 길이와, N ~ 1 번 요소에 대한 LDS 길이의 합은 결국 LBS 길이의 합과 같다.
즉 예외 상황에 대해 아래와 같은 결론을 얻을 수 있다.
S(1) > S(2) > ... S(k-1) > S(k) < S(k+1) ... < S(N-1) < S(N) 일 때, LBS는 S(1) ~ S(k) 또는 S(k) ~ S(N) 이다.
LIS와 LDS의 길이값이 서로 교차하며 증가할 때, 구하고자 하는 값이 구간별 비연속적인 길이값이므로 LBS는 여전히 성립한다.
이제 LIS, LDS 길이를 동시에 구해주자!
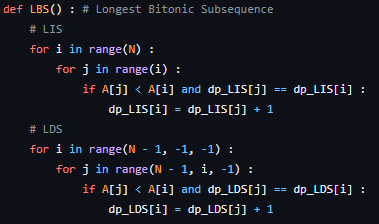
다 구했다면, LBS[i] = LIS[i] + LDS[i] - 1 으로 구할 수 있으며, 이 중 최댓값을 출력해주면 된다.

소스코드
출처
11054번: 가장 긴 바이토닉 부분 수열
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
www.acmicpc.net
'PS > Baekjoon Online Judge' 카테고리의 다른 글
| [백준 9465] 스티커 [Python] (0) | 2023.04.30 |
|---|---|
| [백준 17863] FYI [Python] (0) | 2023.04.30 |
| [백준 11722] 가장 긴 감소하는 부분 수열 [Python] (0) | 2023.04.29 |
| [백준 11053] 가장 긴 증가하는 부분 수열 [Python] (0) | 2023.04.29 |
| [백준 2407] 조합 [Python] (0) | 2023.04.27 |