문제
지민이는 전체 페이지의 수가 N인 책이 하나 있다. 첫 페이지는 1 페이지이고, 마지막 페이지는 N 페이지이다. 각 숫자가 전체 페이지 번호에서 모두 몇 번 나오는지 구해보자.
입력
첫째 줄에 N이 주어진다. N은 1,000,000,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 0이 총 몇 번 나오는지, 1이 총 몇 번 나오는지, ..., 9가 총 몇 번 나오는지를 공백으로 구분해 출력한다.
1019번: 책 페이지
첫째 줄에 0이 총 몇 번 나오는지, 1이 총 몇 번 나오는지, ..., 9가 총 몇 번 나오는지를 공백으로 구분해 출력한다.
www.acmicpc.net
풀이
1부터 N까지의 수에 대해 0부터9가 몇번 나왔는지 구하는 간단한(?) 문제다.
당연히 모든 수에 대해 등장횟수를 구하면 N은 최대 10억으로 시간초과다.
단순하게 시작해 예외를 하나씩 처리했다.
1의 자리부터 시작해 자릿수( digit )를 증가시키며 각 자리수에서 가지는 수를 세주는 방식으로 풀이했다.
우선 아래 그림을 보자.
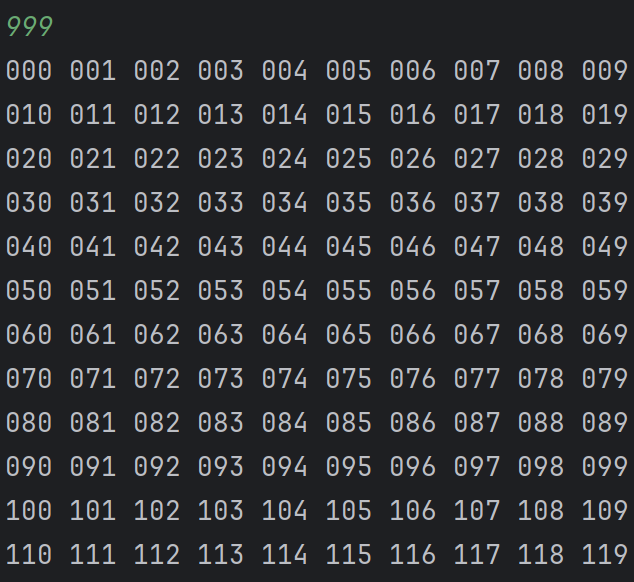
1부터 999까지의 수를 나열했다.
1의 자리에 존재하는 수들은 각각 99 (999 / 10)개가 존재함을 알 수 있다.
nums[i] += N * digit 으로 가정하자.
만약 999까지가 아니라 995면 어떨까?
1부터 5(= R = 995 % 10)까지는 nums[i] += (N + 1) * digit
6(R + 1)부터 9까지는 nums[i] += N * digit 으로 가정하자.

잠깐, 숫자는 1부터 시작한다. 0의 자리는 1개 빼주자.

다음으로 10의 자리에 대해 계산할 차례다.
995를 10으로 나눈 정수값 99에 대해 생각해보자.
편의를 위해 99까지의 수를 보고있다. 여전히 0으로 가득찬 3자리수임을 잊지말자.
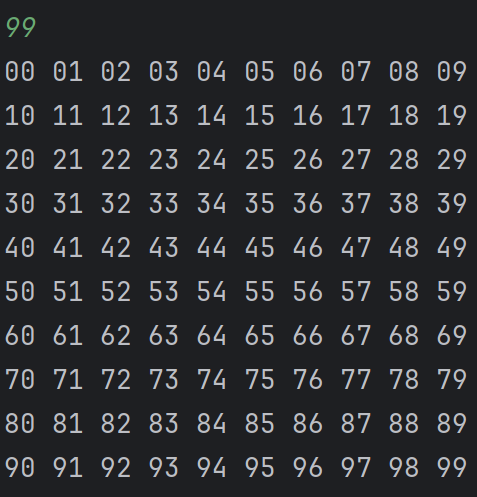
뭔가 이상함을 눈치채야한다.. 0, 1, 2, ... 8 를 포함해 9 또한 갯수가 10개다.
(현재 10의 자리이므로 전체 갯수는 10배를 해준 100을 더해야 한다.)
이대로 계산한다면 995까지가 아닌 999까지 세는것과 동일하다.
N을 감소시키며 숨겨진(hide) 이전 자릿수에 대한 나머지에 대해서도 동일하게 자릿수만큼 곱해주고 더해야 한다.
990, 991, 992, 993, 994, 995이므로 이는 1 + R로 표현할 수 있다.
즉, nums[R] += Q * digit + 1 + R가 성립한다.
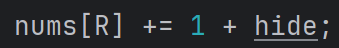
불필요한 0을 제외하자. 00, 01, 02, 03, .... , 09 총 10개다
제거해야 하는 0의 갯수가 늘어난 검사하는 자릿수에 비례한다.

탐색을 진행하며 N은 계속 감소하고 이 과정에서 1의 자리로 밀린 수들은 숨겨질 것이다.
탐색하는 자릿수에 비례해 숨겨질 수들을 기록해 나중에 nums[R]에 더해주자.

소스코드
'PS > Baekjoon Online Judge' 카테고리의 다른 글
| [백준 05340] Secret Location [Python] (0) | 2024.06.18 |
|---|---|
| [백준 01790] 수 이어 쓰기 2 [Java] (0) | 2024.04.10 |
| [백준 01456] 거의 소수 [Java] (1) | 2024.04.06 |
| [백준 06359] 만취한 상범 [Java] (0) | 2024.04.05 |
| [백준 11478] 서로 다른 부분 문자열의 개수 [Python] (1) | 2024.04.01 |