2021. 7. 17. 01:21ㆍPS 풀이/Baekjoon Online Judge

풀이
입력받은 수 num이 num/2 이하의 범위 중에 소수가 존재하는지 몇 줄 내로 간단하게 해결할 수 있지만,
에라토스테네스의 체를 이용해 효율적으로 풀이해봤다.
에라토스테네스의 체는 고대 그리스 수학자 에라토스테네스가 발견한 소수를 구하는 알고리즘이다.
N까지의 수는, N의 제곱근보다 작은 정수들의 배수를 모두 지우고 남는 수가 소수라는 사실을 알 수 있다.
이번 문제에서 주어지는 최대의 자연수는 1000으로, 1000의 제곱근인 31.62xxx보다 작은 정수 31까지의 배수들을 제외하고 남은 수들이 소수임을 알 수 있다.
하지만, 문제에서 입력받는 수가 소수인지 확인하기 위해 탐색하는 과정이 효율적이지 못해 위에서 조작한 배열을 소수와 소수가 아닌 구간으로 정렬해주었다.
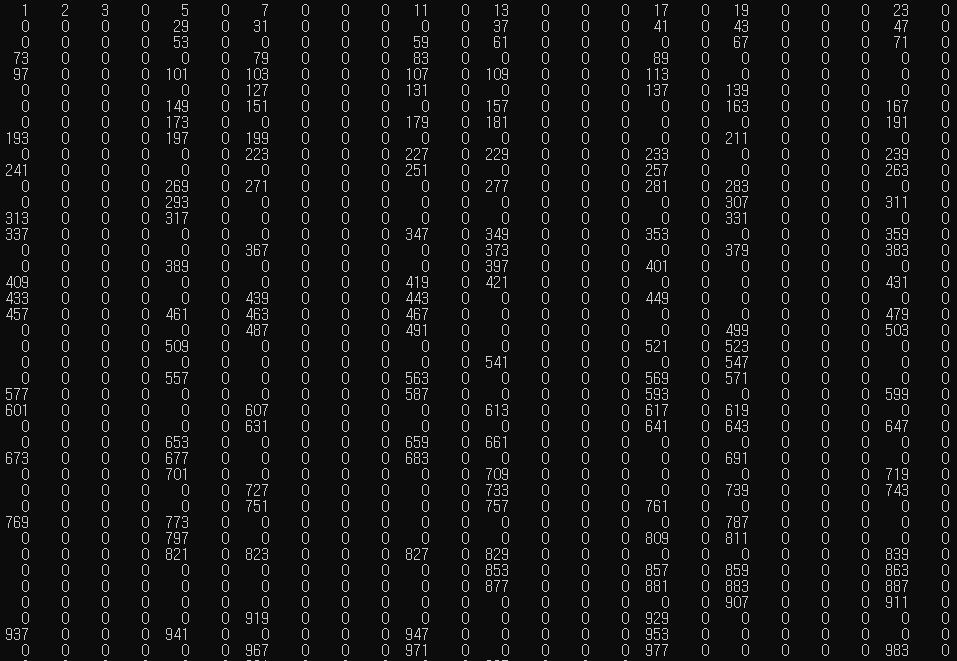
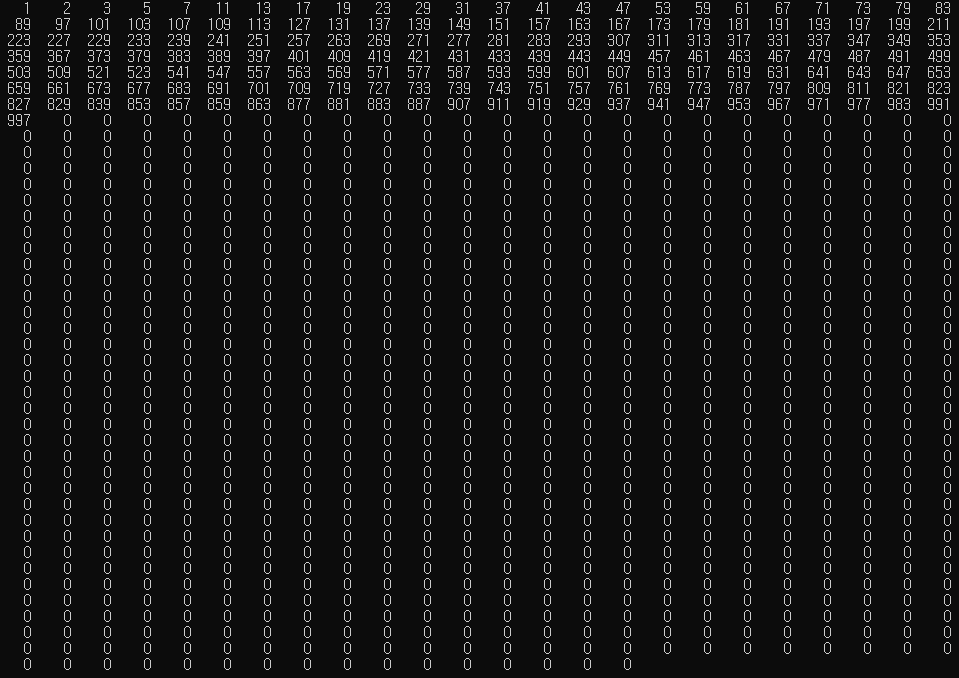
int arr[MAX], idx = 3;
for (int i = 3; i < MAX; i++)
if (arr[i]){
arr[idx++] = arr[i];
arr[i] = 0;
}arr[3] = 4부터 arr[999] = 1000까지의 요소 중, 0이 아니면 현재(i번째) 요소를 idx(맨 처음 0을 가르키는 index이다)번 방에 넣어주고 현재 요소를 0으로 초기화 하는 방법으로 정렬했다.
후에 idx는 입력받은 수가 소수인지 탐색할 때 최대 범위로 사용된다.
소스코드
#include <stdio.h>
#include <math.h>
#define MAX 1000
int main(){
int arr[MAX], idx = 3;
for (int i = 0; i < MAX; i++)
arr[i] = i+1;
for (int i = 2; i <= sqrt(MAX); i++)
if (arr[i-1])
for (int j = i*2; j <= MAX; j += i)
arr[j-1] = 0;
for (int i = 3; i < MAX; i++)
if (arr[i]){
arr[idx++] = arr[i];
arr[i] = 0;
}
int N, prime = 0, num;
scanf("%d", &N);
for (int i = 0; i < N; i++){
scanf("%d", &num);
for (int j = 1; j < idx; j++)
if (num == arr[j])
prime++;
}
printf("%d", prime);
}출처 및 참고자료
1978번: 소수 찾기
첫 줄에 수의 개수 N이 주어진다. N은 100이하이다. 다음으로 N개의 수가 주어지는데 수는 1,000 이하의 자연수이다.
www.acmicpc.net
에라토스테네스의 체 - 위키백과, 우리 모두의 백과사전
수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다. 알고리즘[편집] 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서
ko.wikipedia.org
'PS 풀이 > Baekjoon Online Judge' 카테고리의 다른 글
| [백준 10989] 수 정렬하기 3 [C] (0) | 2021.07.17 |
|---|---|
| [백준 1085] 직사각형에서 탈출 [C] (0) | 2021.07.17 |
| [백준 11651] 좌표 정렬하기 2 [C] (0) | 2021.07.16 |
| [백준 1920] 수 찾기 [C] (0) | 2021.07.15 |
| [백준 11650] 좌표 정렬하기 [C] (0) | 2021.07.15 |