2025. 1. 19. 02:50ㆍPS 풀이/Baekjoon Online Judge
문제
https://www.acmicpc.net/problem/1006
풀이
아마 문제 번호가 1006이거나, 알고리즘 분류에 DP밖에 없어서 많은 분들을 낚은(?) 문제입니다.
평소 DP를 패턴을 찾아 푸시는 분들이라면 많이 어려울 수 있을 것 같습니다.
우선, 특수소대가 구역을 침투하는 방법은 단순합니다.
현재 영역과 인접한 영역의 합이 W보다 작다면 둘 다 점령 아니면 현재 영역만 점령하는 방식입니다.
이 문제는 다음과 같이 나눌 수 있습니다.
- 선형 구조를 점령하기 위해 침투 시켜야 할 특구 소대의 최소 수 구하기
- 원형 구조임을 고려해 초기값을 설정하고 다시 선형 구조를 점령하기
주어진 영역을 원이 아닌 선형 구조로 표현하고,

점령하는 경우의 수는 다음과 같이 3개의 상태로 표현할 수 있습니다.

점화식에 대해서는 다음과 같이 정의하겠습니다.
dp[state][i] : i번째를 점령하는 방법 중 state로 점령했을 때 필요한 최소값
FULL을 구하는 4개의 방법
우선 FULL에 대해 살펴보겠습니다.
dp[FULL][i + 1]을 구하기 위해서는 다음과 같이 4개의 방법이 존재합니다.

1, 2번 방법은 UP, DOWN에 1x1만 추가로 점령하는 경우입니다.

3번 방법은 dp[FULL][i]에 추가로 i + 1번 열의 두 합이 W보다 작은 경우로 2x1만큼 점령한 경우입니다.
모든 단계는 최적의 수라는 보장이 없기 때문에 이전 결과와 항상 비교해야 합니다.

4번 방법은 dp[FULL][i - 1]에 두 소대가 투입되어 1x2 영역을 두개 점령하는 경우입니다.

UP, DOWN을 구하는 2개의 방법
이제 UP, DOWN에 대해서도 계산해야 합니다.
각 상태는 다음과 같이 각 2개의 방법이 존재합니다. 순서대로 UP, DOWN입니다.
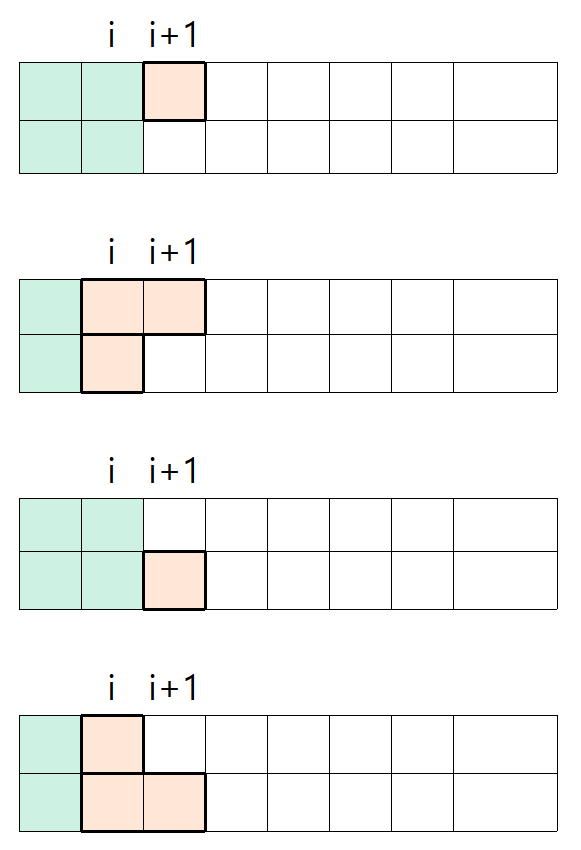
UP, DOWN은 FULL보다 한 칸 앞서 계산하므로 인덱스 검사 후 계산해줍니다.

1, 3번을 미리 계산하고

2, 3번을 이어서 계산하면 됩니다.
여기까지 따라왔다면, 선형 구조에 대해서는 문제를 해결할 수 있습니다.
선형 구조이기 때문에 처음과 끝부분은 원형구조보다 비효율적으로 점령했을 가능성이 높습니다.
이제 원형 구조를 고려해 초기값을 변경해보고 재계산을 해볼 차례입니다.
원형 구조를 고려한 초기값 설정
다음과 같이 3개의 경우에 대해 초기값을 변경하고 재계산해보겠습니다.

각 경우는 ( 0, N - 1 ), ( N, 2N ), { ( 0, N - 1 ), ( N, 2N ) }을 점령한 경우입니다. 3번째 경우는 2x1 또는 1x2로 점령하는 두 경우는 결국 2x2를 점령하는 경우이므로 구분하지 않겠습니다.
우선 1번부터 살펴보겠습니다.
( 0, N - 1 )을 점령한 경우
0, N - 1은 한 소대가 점령할 수 있습니다.
따라서 FULL, UP, DOWN에 대해 초기값이 다음과 같이 변경되어야 합니다.

FULL인 경우 점령되지 않은 N번을 점령합니다.

UP인 경우는 2번과 N번을 점령해야 하는데 인접하지 않으므로 두 소대가 필요합니다.

DOWN인 경우에는 N, N + 1의 합에 따라 필요한 소대의 수가 결정됩니다.

이제 변경된 초기값에 대해 0번 열이 아닌, 1번 열부터 다시 탐색을 진행해야 합니다.
N - 1번 영역은 이미 점령했다 가정하므로, dp[DOWN][N - 1]에 1을 더해준 값과 결과를 비교해주면 됩니다.

( N, 2N )을 점령한 경우
위 방법의 반대로 계산하면 됩니다.
{ ( 0, N - 1 ), ( N, 2N ) } 을 점령한 경우
FULL, UP, DOWN에 대해 다음과 같습니다.
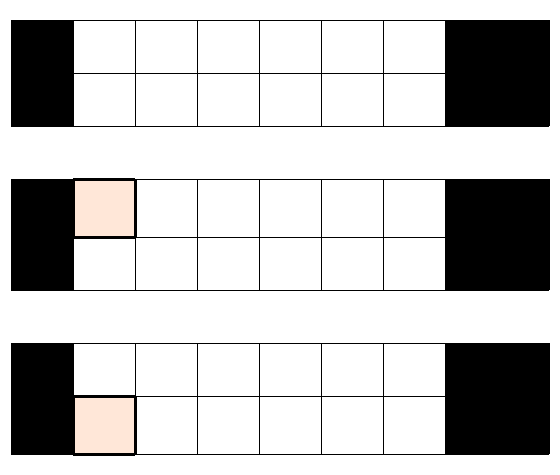
이미 점령된 구간의 수는 나중에 더하므로 FULL에 대해서는 0으로 초기화 합니다.
UP, DOWN 또한 점령할 영역이 1개밖에 없으므로 1로 초기화합니다.
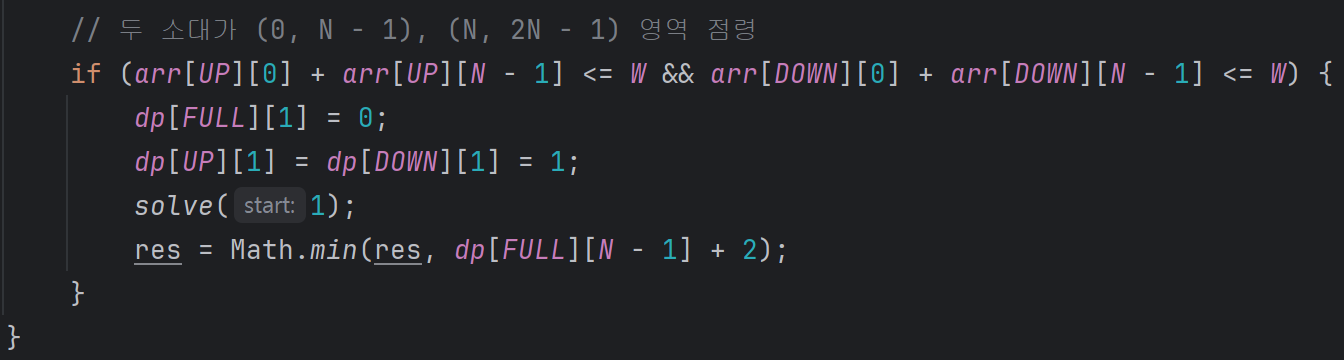
소스코드
'PS 풀이 > Baekjoon Online Judge' 카테고리의 다른 글
| [백준 11438] LCA 2 [Java] (0) | 2025.01.26 |
|---|---|
| [백준 03584] 가장 가까운 공통 조상 [Java] (1) | 2025.01.25 |
| [백준 03653] 영화 수집 [Java] (0) | 2025.01.17 |
| [백준 02533] 사회망 서비스(SNS) [Java] (0) | 2025.01.17 |
| [백준 11966] 2의 제곱인가? [Java] (0) | 2025.01.17 |