2025. 12. 28. 17:23ㆍAlgorithm
CCW란?
세 점 A, B, C가 이루는 회전 방향을 벡터의 외적($\times$, cross product) 부호로 판별하는 기하학적 판별식
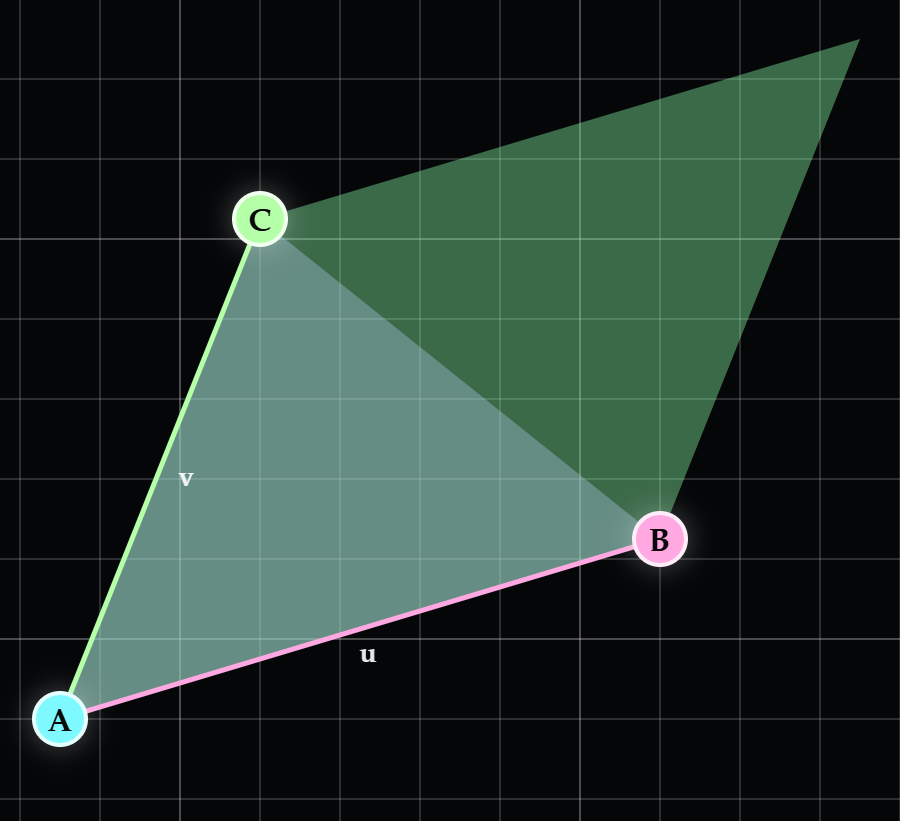
판별식의 결과에 따라 세 점이 이루는 회전 방향은 아래와 같습니다.
 |
 |
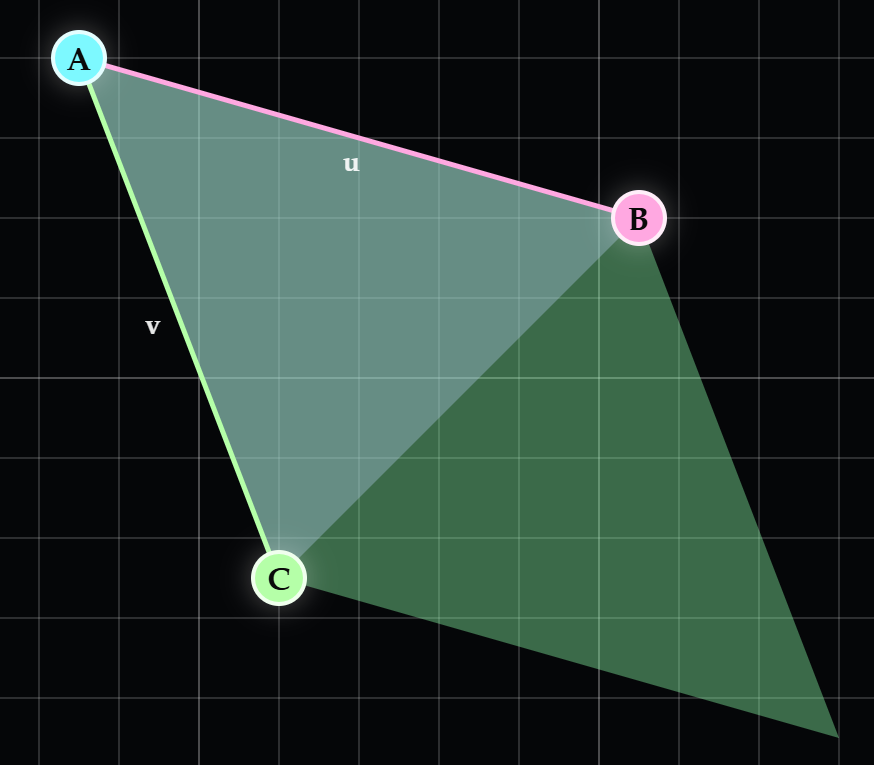 |
| $u \times v > 0$ 반시계(CCW, counterclockwise) |
$u \times v = 0$ 일직선(collinear) |
$u \times v < 0$ 시계(CW, clockwise) |
동작 원리
CCW는 세 점의 각도를 직접 계산하지 않고, 두 벡터 $u, v$가 이루는 상대적인 방향을 외적($\times$) 부호로 판단합니다.
점 A를 기준으로 두 벡터 $u, v$를 정의합니다.
$\vec{AB} = u, \vec{AC} = v$
이때 2차원 벡터의 외적은 다음과 같이 계산됩니다.
$u \times v = u_xv_y - u_yv_x$
이 값은 세 점 A, B, C가 이루는 삼각형의 방향을 나타내며, Graham Scan과 같은 알고리즘에서는 이를 이용해 점 B에서의 좌·우 회전을 판별합니다.
어떻게 두 벡터의 외적으로 CCW를 알 수 있을까?
2차원에서 두 벡터 $u, v$의 외적(cross product)은 두 벡터가 만드는 부호 있는 면적(signed area)에 해당합니다.
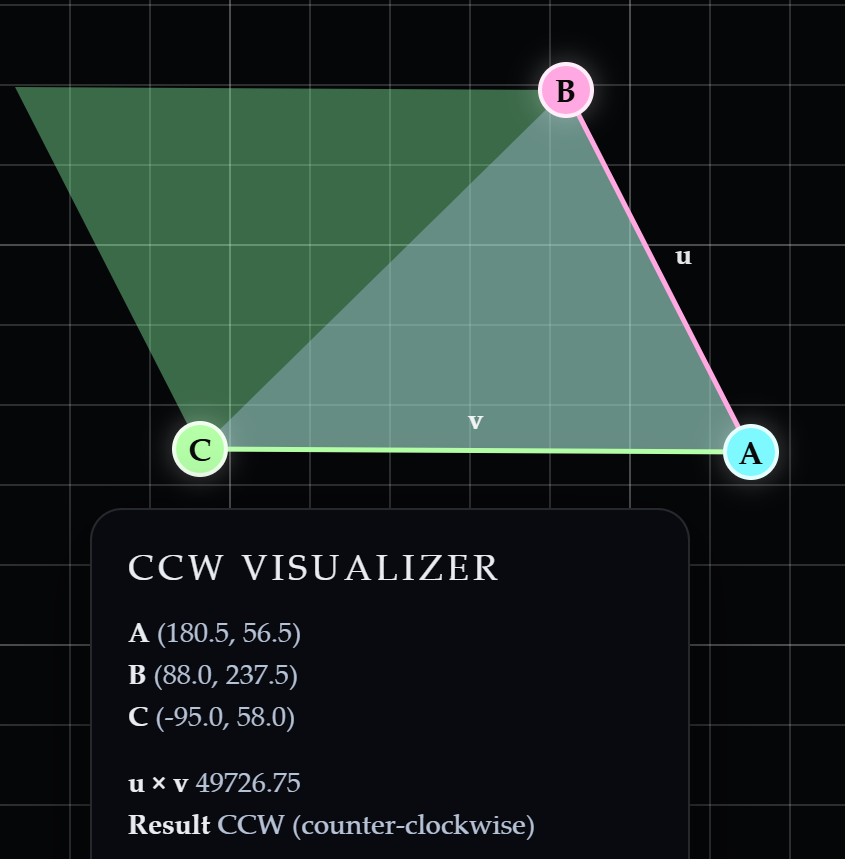
- 외적의 절댓값은 두 벡터가 만드는 평행사변형의 면적을,
- 외적의 부호는 벡터의 나열 순서에 따른 회전 방향을 의미합니다.
따라서 외적의 부호를 확인해 두 벡터가 이루는 회전 방향을 판별할 수 있습니다.
구현
1. (선택) 점(Point) 클래스 선언
점의 위치 정보를 저장할 클래스를 선언합니다.
static class Point {
public final long x, y;
Point(long x, long y) {
this.x = x;
this.y = y;
}
}2. CCW 판별식 구현
세 점을 기준점(A), 방향 기준점(B), 비교점(C) 순서로 입력받는 판별식을 구현합니다.
구현의 단순함과 응용(Graham Scan, Monotone Chain 등)을 위해 기준점 A를 기준으로 구현합니다.
public static int ccw(Point a, Point b, Point c) {
long abx = b.x - a.x;
long aby = b.y - a.y;
long acx = c.x - a.x;
long acy = c.y - a.y;
long cross = abx * acy - aby * acx;
if (cross > 0) return 1;
if (cross < 0) return -1;
return 0;
}
반전된 두 벡터의 CCW 판별
두 벡터를 동시에 반전 하면 외적의 부호는 변하지 않으므로, $\vec{AB} \times \vec{AC}$ 대신 $\vec{BA} \times \vec{CA}$을 사용해도 동일한 CCW 결과를 얻습니다.
$u \times v = (-u) \times (-v)$
따라서 다음과 같이 동치 구현할 수 있습니다.
/*
long abx = b.x - a.x;
long aby = b.y - a.y;
long acx = c.x - a.x;
long acy = c.y - a.y;
*/
long abx = a.x - b.x;
long aby = a.y - b.y;
long acx = a.x - c.x;
long acy = a.y - c.y;
연습 문제
기본 문제
CCW로 세 점 A, B, C의 회전 방향을 판별하는 기본 문제입니다.
'Algorithm' 카테고리의 다른 글
| Stack (0) | 2025.02.19 |
|---|---|
| Sieve of Eratosthenes (0) | 2025.02.19 |
| Euclidean Algorithm (0) | 2025.02.19 |
| LCA, (Lowest Common Ancestor, 최소 공통 조상) (0) | 2025.01.25 |
| Recursive Call (0) | 2024.11.23 |