2026. 1. 31. 17:01ㆍPS 풀이/Baekjoon Online Judge
문제
10272번: 현상금 사냥꾼 김정은
boj.ma
요약
- 모든 점을 한 번씩만 방문
- x좌표는 중복되지 않는다.
- x좌표가 증가하는 순서로 가장 오른쪽 점까지 이동 후 감소하는 순서로 시작점으로 복귀하는 최단 거리를 구하자.
풀이 과정
아이디어
x 좌표가 증가하는 순서로 가장 오른쪽 점까지 이동한 뒤, x 좌표가 감소하는 순서로 시작점(가장 왼쪽 점)으로 돌아오면서, 모든 점을 정확히 한 번씩만 방문하는 비토닉(bitonic) 외판원 순환 문제다.
처음에는 가장 왼쪽 점($L$)과 오른쪽 점($R$)을 잇는 선분을 기준으로 점들을 위·아래로 나누는 방법을 생각할 수 있다.
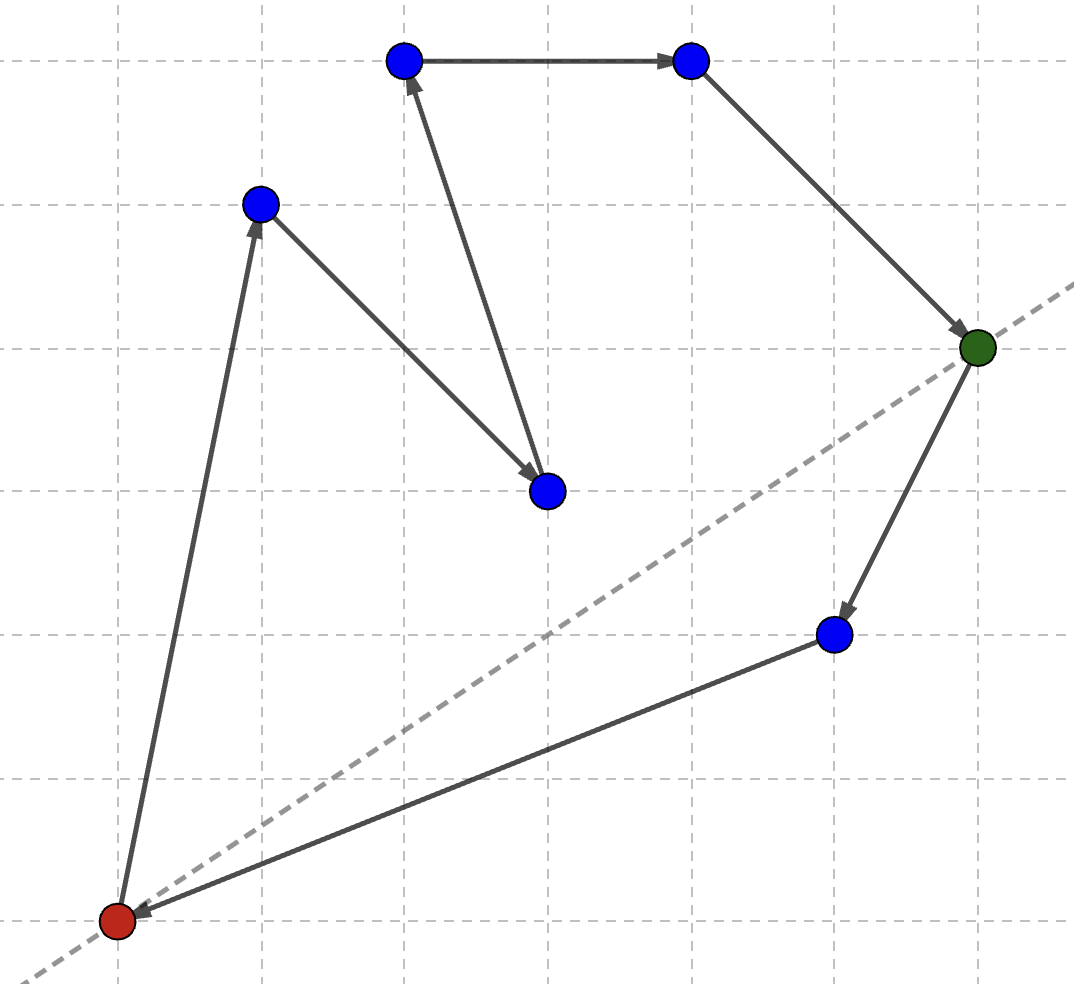
이 경우 비토닉 경로를 만들 수는 있으나, 점들의 실제 거리 관계를 반영하지 못해 항상 최적의 경로를 보장하지 않는다.
다음은 비토닉 경로를 만들면서도, 최단 거리인 경우다.

문제에서 요구하는 폐곡선 형태의 비토닉 순환 경로는, $L$에서 $R$로 향하며 서로 다른 점을 방문하는 두 경로로 볼 수 있다.
i번째 점과 j번째 점 사이의 유클리드 거리 dist[i][j]를 미리 계산해주자.
static double solve(int[] x, int[] y, int N) {
double[][] dist = new double[N][N];
for (int i = 0; i < N; ++i) {
for (int j = i + 1; j < N; ++j) {
double d = Math.hypot(x[i] - x[j], y[i] - y[j]);
dist[i][j] = d;
dist[j][i] = d;
}
}x 좌표 기준으로 0번부터 j번 점까지를 모두 방문했을 때를 다음과 같이 정의했다.
dp[u][d] : 두 경로(위/아래)의 끝점이 u, d일 때의 최소 이동 거리, (u는 d보다 x가 큰 점)
두 경로 중 하나의 경로가 새로운 점을 방문할 때의 최소거리를 갱신해주자.
double[][] dp = new double[N][N];
for (int i = 0; i < N; ++i) Arrays.fill(dp[i], INF);
dp[0][1] = dist[0][1];
for (int d = 2; d < N; ++d) {
int prev = d - 1;
for (int u = 0; u < prev; ++u) {
double cur = dp[u][prev];
if (cur == INF) continue;
// 아래 경로가 다음 점을 선점한 경우
dp[u][d] = Math.min(dp[u][d], cur + dist[prev][d]);
// 윗 경로가 다음 점을 선점한 경우
dp[prev][d] = Math.min(dp[prev][d], cur + dist[u][d]);
}
}모든 점을 방문한 뒤 상태는 dp[i][R] 형태로 끝나며, 마지막으로 두 끝점 i와 R을 연결해 순환 경로를 완성하자. 그 중 최소값이 정답이다.
int last = N - 1;
double ans = INF;
for (int i = 0; i < last; i++) {
ans = Math.min(ans, dp[i][last] + dist[i][last]);
}성능 분석
- 시간 복잡도: $O(N^2)$
- 제출결과: Accepted / 672ms / 140,500KB
참고
문제
10272번: 현상금 사냥꾼 김정은
boj.ma
소스코드
https://github.com/rogi-rogi/problem-solving/blob/main/baekjoon-online-judge/platinum/10272.java
problem-solving/baekjoon-online-judge/platinum/10272.java at main · rogi-rogi/problem-solving
Daily Problem Solving Challenges. Contribute to rogi-rogi/problem-solving development by creating an account on GitHub.
github.com
'PS 풀이 > Baekjoon Online Judge' 카테고리의 다른 글
| [백준 11565] 바이너리 게임 [Java] (0) | 2026.01.13 |
|---|---|
| [백준 23031] 으어어… 에이쁠 주세요.. [Java] (0) | 2026.01.07 |
| [백준 16236] 아기 상어 [Java] (0) | 2026.01.05 |
| [백준 02089] -2진수 [Java] (0) | 2026.01.04 |
| [백준 24727] 인지융~ [Java] (0) | 2026.01.03 |