문제
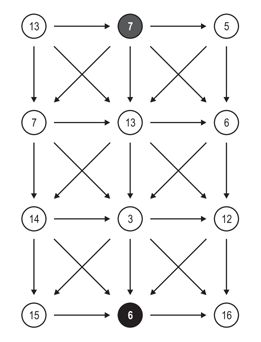
이 문제는 삼각 그래프의 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최단 경로를 찾는 문제이다.
삼각 그래프는 사이클이 없는 그래프로 N ≥ 2 개의 행과 3열로 이루어져 있다. 삼각 그래프는 보통 그래프와 다르게 간선이 아닌 정점에 비용이 있다. 어떤 경로의 비용은 그 경로에서 지나간 정점의 비용의 합이다.
오른쪽 그림은 N = 4인 삼각 그래프이고, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 경로 중 아래로만 가는 경로의 비용은 7+13+3+6 = 29가 된다. 삼각 그래프의 간선은 항상 오른쪽 그림과 같은 형태로 연결되어 있다.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이 순서대로 주어진다. 비용은 정수이며, 비용의 제곱은 1,000,000보다 작다.
입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최소 비용을 테스트 케이스 번호와 아래와 같은 형식으로 출력한다.
k. nk는 테스트 케이스 번호, n은 최소 비용이다.
풀이
주어진 그래프에 대해 순차적으로 탐색하며 최소 비용을 탐색하는 문제다.
가장 위쪽의 왼쪽은 주어지는 정점의 최대 비용보다 크다는 예외를 조심해주자.
dp[f][i] : f층 i번째 정점까지의 최소 비용
문제에서 주어진 그림을 보고 구현만 해주면 된다.
우선, 여러 TC에 대해 입력받자.

처음 시작 위치가 1층 중앙이므로 1층 왼쪽으로는 갈 수 없다. 1층 오른쪽으로 가기 위해서는 중앙 정점의 비용도 합해야 한다.

이제 2 ~ N 층에 대해서도 계산하자.
우선 f층 왼쪽은 f - 1층의 왼쪽과 중앙까지의 누적 비용 중 최솟값을 찾으면 된다.

f층 중앙은 f - 1층의 모든 정점 뿐만 아니라, f층 왼쪽에서 오는 경우도 고려해야 한다.

마찬가지로 f층의 오른쪽은 f - 1층의 중앙과 오른쪽, 그리고 f 층의 중앙에서 오는 경우를 고려하면 된다.

이제 N층의 중앙( dp[N][2] )에 도달하기 위한 최소 비용을 출력하면 된다.
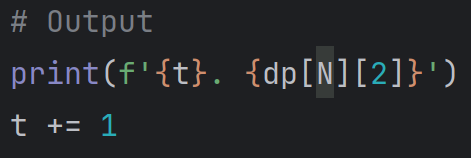
소스코드
출처
'PS > Baekjoon Online Judge' 카테고리의 다른 글
| [백준 02302] 극장 좌석 [Python] (0) | 2024.08.21 |
|---|---|
| [백준 02240] 자두나무 [Python] (0) | 2024.08.21 |
| [백준 15486] 퇴사 2 [Python] (0) | 2024.08.18 |
| [백준 06974] Long Division [Python] (0) | 2024.08.15 |
| [백준 06812] Good times [Python] (0) | 2024.08.08 |